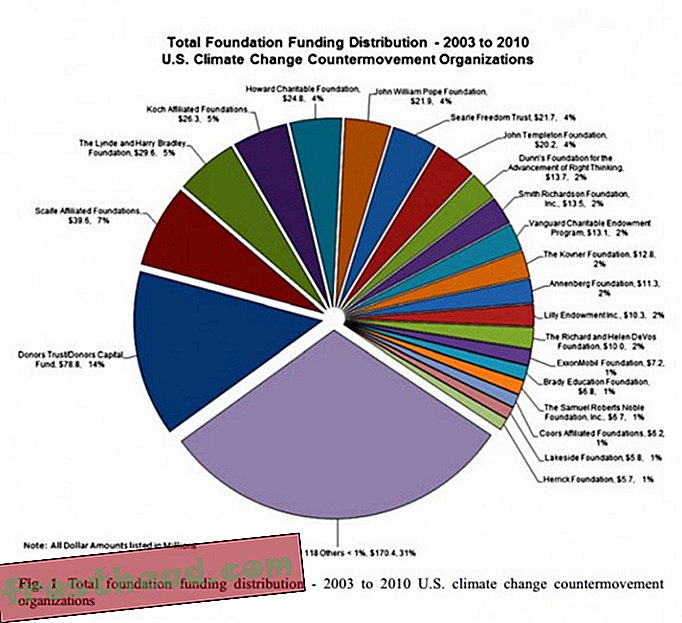
Када већина од нас види машину за вучу која се витла како одмиче на туристичком шеталишту, помислимо на слатки, слатки шећер. Јеан-Луц Тхиффеаулт мисли на слатку, слатку математику. Као примењени математичар са Универзитета Висцонсин-Мадисон, Тхиффеаулт-а је посебно заинтересован за начин на који се материјали попут таффи-а мешају: У машини се бомбони развлаче и пресавијају наново како би унели ваздух и развили своју лагану, жвакаћу текстуру. Како се повлачи, оригинални правокутни правоугаоник растеже се све више и више - његова дужина сваки пут расте експоненцијално за исти омјер. Тај однос растезања је оно што занима Тхиффеаулта.
Сличан садржај
- Растопљена чоколада, 3Д штампане гуме и други фасцинантни патенти за бомбоне
Кад особа извуче јак тен, обично ће узети гомилу слаткиша и развући је на куку, спајајући оба краја. Затим ће узети тај пресавијени комад и поново га развући преко куке, удвостручујући дужину и тако даље. Другим речима, "људски начин рада то је фактор множења 2", каже Тхиффеаулт. Механички уређаји за извлачење могу боље, често доносећи веће, егзотичне ирационалне бројеве као факторе растезања.
Испада да се тачно повлачење може моделирати апстрактним математичким пољем познатим као тополошка динамика, у суштини проучавањем дугорочних, великих промена током времена у математичком простору. (Ако реч тополошка звучи познато, то је недавно било у вестима као део овогодишње Нобелове награде за физику.) Иста математика која описује тачно повлачење такође има озбиљније примене: многи индустријски процеси, укључујући пухање стакла и припрему лекова, захтевају вискозне течности које треба мешати на начине који више личе на повлачење течне него на мешање врхња у кафу. „Ако покушавате да умијешате стварно вискозне ствари, попут пасте за фармацеутску индустрију, не можете их само протрести“, каже Тхиффеаулт. „То није попут мешања боја.“
Тхиффеаулт је дуго времена схватио тачно повлачење као пример вискозног мешања, али тек недавно је заправо проучио историју тачно извлачних метака како би открио своје математичке тајне. Резултат тог излета у историјске патенте је његов недавни рад „Математичка историја чврстих извлакача“, објављен на серверу за штампање арКсив у јулу.
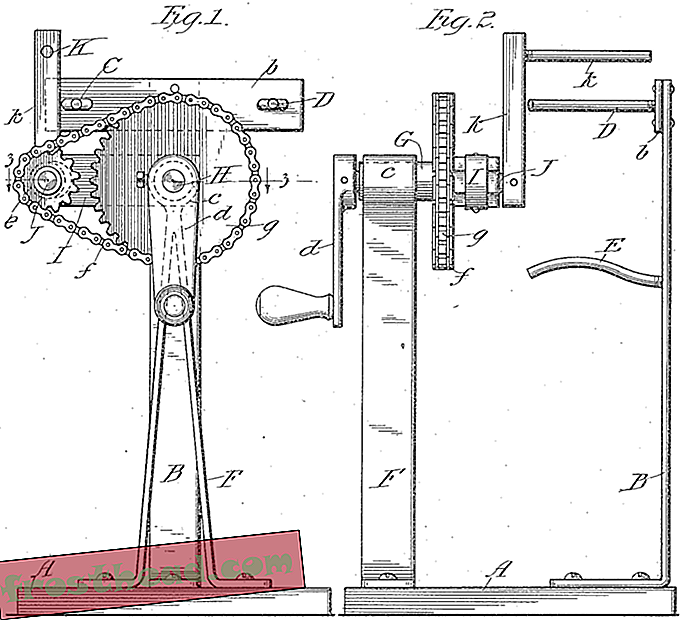Слика из лажне патенте машина из 1916. године која се појављује у Тхиффеаулт студији. Точније, област која је довела до његовог дубоког зарона изузећа је проучавање онога што се назива псеудо-Аносов пресликавањем. Псеудо-Аносов је маштовит начин описивања процеса у којем се дводимензионални облик растеже експоненцијално у једном правцу, док се у другом смањује. Математички је проучавање псеудо-Аносов пресликавања релативно ново. „У 70-им и 80-има људи су се јако трудили да пронађу примере“, каже Тхиффеаулт. Иронично је да су они стално били ту у патентима за привлачне производе. „Будући да математичари никада нису гледали ову литературу, никада не би знали да постоји“, каже он.
Док се чешљао кроз патенте који су били лажни, Тхиффеаулт се нашао у правној битци која је ишла све до Врховног суда. Расправљено у случају из 1921. године, Хилдретх против Мастораса, требало би разумети колико широко треба да се тумачи патент из 1900. године за подмукао поништавач. То је: да ли је неки други модел који је неко други направио само мање побољшање, или је то био другачији уређај? Кључни део аргументације био је колико је патент из 1900. године био различит од претходника из 1893. године (који вероватно никада није произведен). Мишљење суда, чији је аутор главни судија Виллиам Ховард Тафт, „показује снажно разумевање тополошке динамике“, пише Тхиффеаулт у свом чланку.
Суд је признао да ранији уређај - који је имао само две куке - није могао истегнути танак до експоненцијалног степена потребног за ефикасно прављење конфекције. Тафтово мишљење каже:
Са само две кукице није могло доћи до лепљења слаткиша, јер није било трећег игле за поновно активирање бомбона док се држао између друга два игле. Кретање две игле у концентричним круговима може га донекле растегнути и промешати, али не би га повукло у смислу уметности.
Тхиффеаулт пише, "Мишљење Врховног суда показује основни увид да су за постизање некаквог брзог раста потребна најмање три штапа."
Тхиффеаулт каже да се данас користе два стандардна шипка за вучу, један са три штапа и један са четири. Они имају исти фактор истезања. Везана је за такозвани омјер сребра, 1+ √2, односно око 2.414, нешто мање блистав рођак познатијег златног односа.
Чињеница да се два стандардна тањирача повлаче са односом сребра је занимљива јер је омјер сребра - у тачном математичком смислу - оптималан. Међутим, Тхиффеаулт упозорава да није тако лако рангирати различите припијене марамице, чак и кад знате њихове факторе растезања: "Има аспекта јабуке и наранџе према којем је прилично тешко заобићи", каже он. Можда ће један извлакач имати више шипки и требати више времена да се врати у првобитно стање него други или би могао бити потребан већи обртни момент или компликованије пребацивање. Иако математика даје неки увид у то колико добро вуку телади, то не говори у потпуности.
Тхиффеаулт-ово истраживање таффи-пуллерс-а инспирисало је њега и његовог додипломског студента Алека Фланагана да изграде сопствени модел. Желели су да виде да ли могу да повећају ефикасност без промене степена преноса, и на крају су направили нови 6-шипкасти молерски механизам заснован на преносу стандардног 4-шипка. "Разлог зашто смо то успели је тај што сада имамо математику", каже Тхиффеаулт. Могли би да на велико рачунару направе машину и заобиђу пуно покушаја и грешака са стварним физичким уређајима што су раније изумитељи морали да ураде. Уређај са 6 шипки, који је још увек само прототип, растеже се отприлике двоструко више од стандардних извлакача у сваком циклусу.
До сада, произвођачи лажних товара нису баш тукли Тхиффеаултова врата да би добили његов савет о оптимизацији дизајна - Биг Таффи је очигледно задовољан својим растезљивим статусом куо - али нада се да би његове методе могле имати ефекта у другим индустријама. Поред пухања стакла, једно логично место за оптимизацију мешања је фармацеутска индустрија. На крају крајева, мешање витамина и лекова захтева изузетно високу контролу квалитета: Произвођачи су „спремни платити пуно новца за савршено мешање“, јер „не могу да подносе један лош мултивитамин од 1000“, каже Тхиффеаулт. Тако ће једног дана фармацеути можда слатко узвикивати одане тешке призиваче.
Онда опет, то би могло бити мало потезање.
